微观天下

发表于 更新于 分类于

数组

时间复杂度

操作 时间复杂度
查询 Lookup O(1)
插入 Insert O(n)
删除 Delete O(n)
前插 Prepend/Pushfront O(n)
后插 Append/Pushback O(1)

删除有序数组中的重复项

LC26题目链接

1
2
3
4
5
6
7
8
9
10
11

class Solution {
    public int removeDuplicates(int[] nums) {
        int cur = 0;
        for(int i = 1; i < nums.length; i++ ) {
            if(nums[i] != nums[cur]) nums[++cur] = nums[i];//如果当前nums[i]的值与已经存储的最后元素nums[cur]不等，则存入下一个位置, 第一个数肯定要
        }
        return cur+1;
    }
}

移动零

LC283题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution {
    public void moveZeroes(int[] nums) {
        int cur = 0;
        for(int i = 0; i < nums.length; i ++) {
            if(nums[i] != 0) nums[cur++] =  nums[i];
        }

        //补零
        while ( cur < nums.length ) {
            nums[cur] = 0;
            cur ++;
        }
    }
}

合并两个有序数组

LC88题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m -1, j = n -1, cur = m + n -1;
        while(i >= 0 || j >= 0) {
            if(j < 0 || (i >= 0 && nums1[i] >= nums2[j])){ // 在nums2已经越界或者i没越界且为大的时候，存入nums1[i]
                nums1[cur] = nums1[i];                
                i--;
            } else {
                nums1[cur] = nums2[j];
                j--;
            }
            cur--;
        }
    }
}

变长数组ArrayList设计题

如何实现一个变长数组？

  • 支持索引与随机访问
  • 分配多长的连续空间
  • 空间不够用了怎么办
  • 空间剩余很多如何回收

链表

单链表和双链表数据结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

// 单链表
class MyLinkedListNode {
    int val;
    MyLinkedListNode next;
}

// 双链表
class MyDoubleLinkedListNode {
    int val;
    MyDoubleLinkedListNode next;
    MyDoubleLinkedListNode pre;
}


public static void main(String[] args) {
    // 具有保护节点的单链表 protect.next = head
    LinkedList protect = new LinkedList(0, null);

    // 

    // 具有保护节点组的双链表      
    LinkedList protectTail = new LinkedList(0, null);        
    LinkedList protectHead = new LinkedList(0, protectTail);
    protectTail.pre = proctedHead;
    protectedHead.pre = null;
}

时间复杂度

操作 时间复杂度
查询 Lookup O(n)
插入 Insert O(1)
删除 Delete O(1)
前插 Prepend/Pushfront O(1)
后插 Append/Pushback O(1)

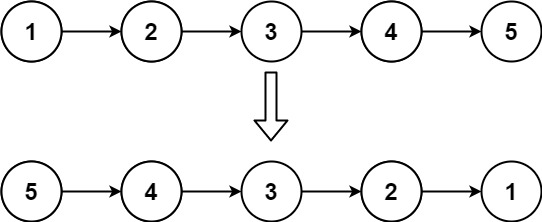
反转链表问题

LC206题目链接

LC206

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode last = null;
        while (head != null) {
            ListNode nextHead = head.next; // 缓存因为next会被修改
            head.next = last; // 跟新next指针
            last = head; //更新上一个节点为当前节点
            head = nextHead; // 更新当前节点 推进
        }

        return last;
    }
}

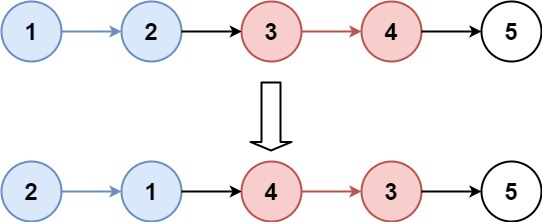
K个一组翻转链表

LC25题目链接

LC25

解题思路

  • 分组：每k个元素的头尾节点确定
  • 子问题：针对每一组k个元素的反转问题
  • 每组k个元素的前驱后继引用更新问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
    ListNode protect = new ListNode(0, head);
    ListNode last = protect;
    while(head != null) {
        // 1. 分组：每k个元素的头尾节点确定
        ListNode groupEnd = getEnd(head, k);
        if(groupEnd == null) break;
        // 分组遍历逻辑
        ListNode cacheNexthead = groupEnd.next; // 后继结点会被跟新需要先缓存
        
        
        // 2. 子问题：针对每一组k个元素的反转问题
        reverseList(head, cacheNexthead);

        // 3. 每组k个元素的指向前一组tail，后一组head引用更新问题        
        last.next = groupEnd; // 前一组最后应指向本组的最后即变化后的头节点
        head.next = cacheNexthead; // 本组的最后一个节点应该指向下一组的head

         // 更新组头尾节点
            last = head; // last 应该指向调转后的head，groupEnd已经是新的链表头
            head = cacheNexthead; // head 应该指向下一组头节点
        }

        return protect.next;
    }

    public ListNode getEnd(ListNode head, int k) {
        while (head != null) {
            k--;            
            if(k == 0) return head;
            head = head.next; // 走k-1次，返回groupEnd
        }
        // 返回End, 但是复用LC206算法需要last.next
        return head;
    }

    public void reverseList(ListNode head, ListNode nextHead) {
        // 第一步跳过，因为第一个head的next会在第三步更新
        ListNode last = head;
        head = head.next;
        while (head != nextHead) {
            ListNode cacheNextHead = head.next; // 缓存因为next会被修改
            head.next = last; // 跟新next指针
            last = head; //更新上一个节点为当前节点
            head = cacheNextHead; // 更新当前节点 推进
        }
    }
}

邻值查找/双链表问题

ACWing题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

import java.util.Arrays;
import java.util.Scanner;

// ACWing need a class called Main for solution
// and all the input/output logic
public class Main {

    public static void main(String args[]) {
        // input the array
        Scanner sc = new Scanner(System.in);
        int size = sc.nextInt();
        int i = 0;
        Node[] nums = new Node[size], sorted = new Node[size];
        int[] diff = new int[size-1], pre = new int[size-1];
        while(i < size){
            int number = sc.nextInt();
            Node node = new Node(number, i);
            nums[i] = node;
            sorted[i] = node;
            i++;
        }
        // sort and add pre/post information to build a linked list;
        Arrays.sort(sorted);
        for(int j = 0; j < sorted.length; j++){
            if(j > 0) sorted[j].pre = sorted[j-1]; else sorted[j].pre = new Node(Integer.MIN_VALUE, -1);
            if(j < nums.length -1) sorted[j].post = sorted[j+1]; else sorted[j].post = new Node(Integer.MAX_VALUE, size);
        }

        // start from last of array nums, calc it's pre/post diff via Linked List, and remove that node in linked list;
        while(i > 1){
            i--;
            int preDiff = nums[i].pre.index >= 0 && nums[i].pre.index < size ? nums[i].value - nums[i].pre.value : Integer.MAX_VALUE;
            int postDiff = nums[i].post.index >= 0 && nums[i].post.index < size ? nums[i].post.value - nums[i].value: Integer.MAX_VALUE;
            diff[i-1] = Math.min(preDiff, postDiff);
            if(preDiff <= postDiff) pre[i-1] = nums[i].pre.index+1;
            else pre[i-1] =  nums[i].post.index+1;
            removeNode(nums[i]);
        }

        print(diff, pre);
    }

    private static void print(int[] diff, int[] pre){
        for(int i = 0; i < diff.length; i++){
            System.out.println(diff[i] + " " + pre[i]);
        }
    }

    private static void removeNode(Node node){
        Node postCache = node.post;
        node.pre.post = postCache;
        node.post.pre = node.pre;
    }

    static class Node implements  Comparable<Node>{
        int value;
        int index;
        public Node pre;
        public Node post;

        public Node(int value, int index){
            this.value = value;
            this.index = index;
        }


        @Override
        public int compareTo(Node other) {
            return this.value - other.value;
        }
    }
}

链表找环问题

LC141题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        do {
            if(fast == null || fast.next == null) return false; 
            fast = fast.next.next; // 快指针每次走两步
            slow = slow.next; // 慢指针每次走一步
        }
        while(fast != slow);
        return true;
    }
}

LC142题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        do {
            if(fast == null || fast.next == null) return null; 
            fast = fast.next.next; // 快指针每次走两步
            slow = slow.next; // 慢指针每次走一步
        }
        while(fast != slow);
        ListNode slow2 = head; 
        while (slow != slow2){ // 不能do while，因为有可能相遇的节点就正是环开始节点 [1, 2] 0
            slow = slow.next;
            slow2 = slow2.next;
        }
        return slow;
    }
}

合并两个有序链表

LC21题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode cur1 = list1, cur2 = list2, nextHead2 = null, protect = new ListNode(0, list1),lastHead1 = protect;
        while(cur1 != null || cur2 != null) {           
            // 更新节点
            if(cur1 == null || (cur2 != null && cur1.val > cur2.val)){ // 取list2节点,cur2 推进
                // 先缓存即将推进的节点
                nextHead2 = cur2.next;
                // cur2 插入在cur1之前,lastHead1之后       
                cur2.next = cur1;               
                lastHead1.next = cur2;
                // 更新lastHead1 和cur2 指针          
                lastHead1 = cur2;
                cur2 = nextHead2;                
            } else { //取list1节点，cur1直接推进
                lastHead1 = cur1;
                cur1 = cur1.next;
            }
        }
        return protect.next;
    }
}

加一

LC66题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    public int[] plusOne(int[] digits) {
        // 逆序+递归
        return plusOne(digits, digits.length -1);
    }

    public int[] plusOne(int[] digits, int pos){
        if(pos == -1) {
            int[] result = new int[digits.length+1];
            result[0] = 1;
            for(int i = 0; i < digits.length; i ++){
                result[i+1] = digits[i];
            }
            return result;
        }
        digits[pos] += 1;
        if(digits[pos]/10 == 1) {
            digits[pos] %= 10;
            return plusOne(digits, pos-1);
        }
        return digits;
    }
}

栈

后缀表达式求值

LC150题目链接

解题思路

建立一个用于存数的栈，逐一扫描后缀表达式中的元素。

  • 如果遇到一个数，则把该数入栈。
  • 如果遇到运算符，就取出栈顶的两个数进行计算，然后把结果入栈。
    扫描完毕后，栈中恰好剩下的一个数，就是该表达式的值。

时间复杂度为O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    public int evalRPN(String[] tokens) {
            int cur = 0;
            Stack<Integer> nums = new Stack<>();
            while(cur < tokens.length){
                if(tokens[cur].equals("+") || tokens[cur].equals("-") || tokens[cur].equals("*")  || tokens[cur].equals("/")){
                Integer operant1 = nums.pop();
                Integer operant2 = nums.pop();
                nums.push(calculate(operant1, operant2, tokens[cur]));
            }else nums.push(Integer.parseInt(tokens[cur]));
                cur ++;
            }
            return nums.peek();
        }

        public Integer calculate(Integer x, Integer y, String operator){
            switch(operator)
            {
                case "+":
                    return x + y;
                case "-":
                    return y - x;
                case "*":
                    return x * y;
                case "/":
                    return y/x;
            }
            return 0;
        }
}

中缀表达式：基本计算器I & II

LC227题目链接

解题思路一

中缀转后缀，然后计算：

  • 需要看下一个符号的优先级是否高于本符号。
  • 如果高于：需要一个操作符栈，低优先级符号先入栈，高优先级的符号后入栈，先出。
  • 如果低于：把操作符栈出放入后缀表达式队列。
  • 处理后缀表达式队列，参考上题。

3+2*2

运算符栈： + *

后缀表达式： 3 2 2 * +

3+2-2

运算符栈：

后缀表达式： 3 2 + 2 -

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
class Solution {
   public int calculate(String s) {
            s += " ";
            ArrayList<String> tokens = new ArrayList<>();
            Stack<Character> operators = new Stack<>();
            String number = "";
            boolean needsZero = true; // -4 * 9 需要补零
            for(int i = 0; i < s.length(); i ++){
                char ch = s.charAt(i);
                if (ch >= '0' && ch <= '9'){
                    number += ch;
                    needsZero = false; // 5-3 不需要补零
                    continue;
                } else if(!number.isEmpty()){
                    tokens.add(number);
                    number = "";
                }

                if (ch == ' ') continue;
                if (ch == '(') {
                    operators.push('(');
                    needsZero = true; // (-3) 需要补零
                    continue;
                }
               if (ch == ')') {
                    while (!operators.empty() && !operators.peek().equals('(')){
                        tokens.add(operators.pop().toString());
                    }
                    if (!operators.empty() && operators.peek().equals('(')){
                        operators.pop();// 不需要）
                    }
                    needsZero = false; // )-3 不需要补零
                    continue;
                }

                int currRank = getRank(ch);
                while (!operators.empty() && getRank(operators.peek()) >= currRank){
                    tokens.add(operators.pop().toString());
                }
                operators.push(ch);
                if(ch == '-' && needsZero) tokens.add(Integer.toString(0));
            }

            while (!operators.isEmpty()){
                tokens.add(operators.pop().toString());
            }

            return evalRPN(tokens);
        }

        public int getRank(char ch){
            if(ch == '+' || ch == '-' ) return 1;
            if(ch == '*' || ch == '/' ) return 2;
            return 0;
        }

        int evalRPN(ArrayList tokens){
            Stack<Integer> operants = new Stack<>();
            for(int i = 0; i < tokens.size(); i ++ ){
                String token = (String) tokens.get(i);
                if(token.equals("+") || token.equals("-") || token.equals("*") || token.equals("/")){
                    Integer operant1 = operants.pop();
                    Integer operant2 = operants.pop();
                    operants.push(calc(operant1, operant2, token));
                }else {
                    operants.push(Integer.parseInt(token));
                }
            }
            return operants.peek();
        }

        Integer calc(Integer x, Integer y, String token){
            if(token.equals("+")) return x +y;
            if (token.equals("-")) return y -x;
            if(token.equals("*")) return x *y;
            if (token.equals("/")) return y /x;
            return 0;
        }
}

解题思路二

表达式拆分，加减运算为低优先级运算，将操作数和符号一起入栈。乘除为高优先级运算，遇到则立刻处理。最后将所有操作数出栈相加，得到结果。

LC224题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

class Solution {
   public int calculate(String s) {
            s += " ";
            ArrayList<String> tokens = new ArrayList<>();
            Stack<Character> operators = new Stack<>();
            String number = "";
            boolean needsZero = true; // -4 * 9 需要补零
            for(int i = 0; i < s.length(); i ++){
                char ch = s.charAt(i);
                if (ch >= '0' && ch <= '9'){
                    number += ch;
                    needsZero = false; // 5-3 不需要补零
                    continue;
                } else if(!number.isEmpty()){
                    tokens.add(number);
                    number = "";
                }

                if (ch == ' ') continue;
                if (ch == '(') {
                    operators.push('(');
                    needsZero = true; // (-3) 需要补零
                    continue;
                }
               if (ch == ')') {
                    while (!operators.empty() && !operators.peek().equals('(')){
                        tokens.add(operators.pop().toString());
                    }
                    if (!operators.empty() && operators.peek().equals('(')){
                        operators.pop();// 不需要）
                    }
                    needsZero = false; // )-3 不需要补零
                    continue;
                }

                int currRank = getRank(ch);
                while (!operators.empty() && getRank(operators.peek()) >= currRank){
                    tokens.add(operators.pop().toString());
                }
                operators.push(ch);
                if(ch == '-' && needsZero) tokens.add(Integer.toString(0));
            }

            while (!operators.isEmpty()){
                tokens.add(operators.pop().toString());
            }

            return evalRPN(tokens);
        }

        public int getRank(char ch){
            if(ch == '+' || ch == '-' ) return 1;
            if(ch == '*' || ch == '/' ) return 2;
            return 0;
        }

        int evalRPN(ArrayList tokens){
            Stack<Integer> operants = new Stack<>();
            for(int i = 0; i < tokens.size(); i ++ ){
                String token = (String) tokens.get(i);
                if(token.equals("+") || token.equals("-") || token.equals("*") || token.equals("/")){
                    Integer operant1 = operants.pop();
                    Integer operant2 = operants.pop();
                    operants.push(calc(operant1, operant2, token));
                }else {
                    operants.push(Integer.parseInt(token));
                }
            }
            return operants.peek();
        }

        Integer calc(Integer x, Integer y, String token){
            if(token.equals("+")) return x +y;
            if (token.equals("-")) return y -x;
            if(token.equals("*")) return x *y;
            if (token.equals("/")) return y /x;
            return 0;
        }
}

柱状图中最大的矩形

LC84题目链接

单调栈算法, 维护一个单调递增高度的栈，当一个新的高度低于当前栈顶时，单调性被破坏，需要将被破坏的栈元素逐个出栈，直到入栈新元素时单调性恢复。出栈元素的宽度元素叠加到accumulatedWidth中，以被后面的元素可以计算矩形面积。时间复杂度时O(n)。

思维套路

  • 确定递增递减——关键在于考虑“前面不能影响到后面”的条件
  • 本题中若h[i-1]>h[i], 则h[i-1]这个高度就无法影响到后面，自然可以单独计算了

代码套路

  • for每个元素
    • while（栈顶与新元素不满足单调性）{弹栈，更新答案，累加“宽度”}
    • 入栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int largestRectangleArea(int[] heights) {
            Stack<Rect> s = new Stack<>();
            int result = 0;
            for(int i = 0; i <= heights.length; i ++){
                int h = i == heights.length ? 0 : heights[i]; // 末尾补零，从而清空栈。
                int accumulatedWidth = 0;
                // 新的元素破坏单调性
                while(!s.isEmpty() && s.peek().height > h) {
                    accumulatedWidth += s.peek().width;
                    result = Math.max(result, s.peek().height * accumulatedWidth);
                    s.pop();
                }
                s.push(new Rect(accumulatedWidth + 1, h));
            }
            return result;
        }

        class Rect {
            int width;
            int height;

            Rect (int width, int height){
                this.width = width;
                this.height = height;
            }
        }
}

接雨水

LC42题目链接

思维套路

  • 确定递增递减——关键在于考虑“前面不能影响到后面”的条件
  • 本题中若h[i-1]< h[i], 则h[i-1]这个高度就无法影响到后面，自然可以单独计算了

单调递减栈算法：维护一个单调递减的栈，当栈顶高度小于新入栈元素的高度时，弹出所有小于新入栈元素的元素，然后累计弹出元素的横条面积，其中横条面积是一个以栈顶为底和宽度，栈顶元素前后的最小值为高的长方形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
        public int trap(int[] heights) {
            int result = 0;
            for(int i = 0; i < heights.length; i++){
                int accumulatedWidth = 0;
                int height = heights[i];
                while(!s.isEmpty() && s.peek().height <= height) {
                    int bottom = s.peek().height;
                    accumulatedWidth += s.peek().width;
                    s.pop();
                    // 以bottom为底，accumulatedWidth为宽度，（左右两侧较小者）up为顶的长方形是累积的雨水横条
                    // 如果栈空，则高度为bottom，增加面积为0
                    int up = s.isEmpty() ? bottom : Math.min(height, s.peek().height);

                    result += accumulatedWidth * (up - bottom);
                }
                s.push(new Rect( accumulatedWidth + 1, height ));
            }
            return result;
        }

    class Rect {
        int width;
        int height;
        Rect(int width, int height){
                this.width = width;
                this.height = height;
            }
    }

    Stack<Rect> s = new Stack<>();
}

有效的括号

LC20题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public boolean isValid(String s) {
        for(int i = 0; i < s.length(); i++){
            char c = s.charAt(i);
            if(c == ')'){
                if(o.isEmpty() || !cleanUp("(")) return false;
            }else if(c == '}'){
                if(o.isEmpty() || !cleanUp("{")) return false;
            }else if(c == ']'){
                if(o.isEmpty() || !cleanUp("[")) return false;
            }else o.push(String.valueOf(c));
        }
        if(o.isEmpty()) return true;
        return false;
    }

    private boolean cleanUp(String match){
        while(!o.isEmpty()) {
            String x = o.pop();
            if(x.equals(match)) return true;
            else return false;
        }
        return false;
    }
    Stack<String> o = new Stack<>();
}

最小栈

LC155题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

class MinStack {

    public MinStack() {

    }
    
    public void push(int val) {
        // 单调递减栈
        if(min.isEmpty() || (!min.isEmpty() && min.peek() >= val)) {
            min.push(val);
        }
        s.push(val);
    }
    
    public void pop() {
        if(s.pop().equals(min.peek())) min.pop();
    }
    
    public int top() {
        return s.peek();
    }
    
    public int getMin() {
        return min.peek();
    }

    // 单调递减栈
    private Stack<Integer> min = new Stack<>();
    // 原栈
    private Stack<Integer> s = new Stack<>();
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

队

滑动窗口最大值

LC139题目链接

思维套路

  • 单调队列维护的是一个候选集和，前面的较旧，后边比较新（时间有单调性）
  • 候选项的某个属性也具有单调性（比如整数值）
  • 确定递增递减的方法——考虑任意连个候选项j1< j2，写出j1比j2优的条件

排除冗余的关键：若j1比j2差（nums[j1]< nums[j2]，且j1的生命周期比j2短，那j1就没有留在队列中的意义。

单调递减队列：需要维护一个单调递减队列，队尾插入新元素，当新元素大于队尾元素时，队尾元素出栈，直到满足单调条件。队首元素需要满足索引大于i-k条件。

代码套路

  • for每个元素
    1. while(队头过期) 队头出队
    2. 取队头为最佳选项，计算答案
    3. while（队尾与新元素不满足单调性）队尾出队
    4. 新元素入队

2和3的顺序取决于i是不是候选项。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
        public int[] maxSlidingWindow(int[] nums, int k) {
            int[] result = new int[Math.max(nums.length - k + 1, 1 )];
            int cur = 0;
            for(int i = 0; i < nums.length; i ++){
                int number = nums[i];
                while(!q.isEmpty() && nums[q.peekFirst()] <= i - k) q.removeFirst();
                while(!q.isEmpty() && nums[q.peekLast()] < number) q.removeLast();

                q.add(i);
                // 单调递减队列，队首是最大值
                if(i >= k-1)  result[cur++] = nums[q.peekFirst()];
            }
        return result;
        }

        LinkedList<Integer> q = new LinkedList<>();
    }

设计循环双端队列

LC641题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class MyCircularDeque {

    public MyCircularDeque(int k) {
            q = new LinkedList<Integer>();
            capacity = k;
        }

        public boolean insertFront(int value) {
            if(q.size() == capacity) return false;
            q.addFirst(value);
            return true;
        }

        public boolean insertLast(int value) {
            if(q.size() == capacity) return false;
            q.addLast(value);
            return true;
        }

        public boolean deleteFront() {
            if(q.isEmpty()) return false;
            q.removeFirst();
            return true;
        }

        public boolean deleteLast() {
            if(q.isEmpty()) return false;
            q.removeLast();
            return true;
        }

        public int getFront() {
            return q.isEmpty()? -1 : q.peekFirst();
        }

        public int getRear() {
            return q.isEmpty()? -1 : q.peekLast();
        }

        public boolean isEmpty() {
            return q.isEmpty();
        }

        public boolean isFull() {
            return q.size() == capacity;
        }

        private LinkedList<Integer> q ;
        private int capacity;
}

/**
 * Your MyCircularDeque object will be instantiated and called as such:
 * MyCircularDeque obj = new MyCircularDeque(k);
 * boolean param_1 = obj.insertFront(value);
 * boolean param_2 = obj.insertLast(value);
 * boolean param_3 = obj.deleteFront();
 * boolean param_4 = obj.deleteLast();
 * int param_5 = obj.getFront();
 * int param_6 = obj.getRear();
 * boolean param_7 = obj.isEmpty();
 * boolean param_8 = obj.isFull();
 */

最大矩形

LC85题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution {
    public int maximalRectangle(char[][] matrix) {
        // 构造纵向连续1和二维数组S[rows][cols]
        // S[p][] 是一组子矩阵的纵向柱状图，求出最大矩形
        // 遍历所有p，得出最大矩阵所包含的最大矩形
        int rows = matrix.length, cols = matrix[0].length;
        int[][] S = new int[rows+1][cols];
        int[] max = new int[rows];
        int ans = 0;
        for(int r = 0; r <= rows; r ++) {            
            for(int c = 0; c < cols; c++) {
                if( r == 0 || matrix[r-1][c] == '0') {
                    S[r][c] = 0;
                    continue;
                } else S[r][c] = S[r-1][c]+1;
            }
        }

            for(int r = 1; r <= rows; r++) {
                max[r-1] = largestRectangleArea(S[r]);
                ans = Math.max(ans, max[r-1]);
            }

        return ans;
    }

    public int largestRectangleArea(int[] heights) {
            Stack<Rect> s = new Stack<>();
            int result = 0;
            for(int i = 0; i <= heights.length; i ++){
                int h = i == heights.length ? 0 : heights[i];  // 末尾补零，从而清空栈。
                int accumulatedWidth = 0;
                // 新的元素破坏单调性
                while(!s.isEmpty() && s.peek().height > h) {
                    accumulatedWidth += s.peek().width;
                    result = Math.max(result, s.peek().height * accumulatedWidth);
                    s.pop();
                }
                s.push(new Rect(accumulatedWidth + 1, h));
            }
            return result;
        }

        class Rect {
            int width;
            int height;

            Rect (int width, int height){
                this.width = width;
                this.height = height;
            }
        }
}

前缀和

前缀和思想是运用前缀和数组作为桥梁，取解决数组的各种子数组优化问题。已知数组A[ i]，

s[ i] = s[ i - 1] + A[ i]

字段和从l 到 r则表达为：

sum(l, r) = s[ r] - s[ l - 1]

当A中都是非负数时，前缀和数组s单调递增。这样子数组和问题就转化成了s数组元素的问题。

统计优美子数组

LC1248题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int numberOfSubarrays(int[] nums, int k) {
        int[] s = new int[nums.length+1];
        s[0] = 0;
        int[] count = new int[nums.length+1];
        count[0] = 1;
        for(int i = 1; i < count.length; i ++) count[i] = 0;
        for(int i = 1; i <= nums.length; i++) {
            s[i] = s[i-1] + nums[i-1]%2;
            count[s[i]]++;
        }
        // 存入count[s[i]]的个数
        // s[i] - s[j] == k 等价于
        // count[s[i] - k] 的个数
        int result = 0;
        for(int i = 0; i < s.length; i ++ ) {
            if(s[i] >=k ) result += count[s[i] - k];
        }
        return result;
    }
}

最大子序和

LC53题目链接

解题思路一

通过维护前缀和数组，和前缀最小和数组，两者差为子数组和，求最大值问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
    public int maxSubArray(int[] nums) {
        int[] s = new int[nums.length+1];
        s[0]=0;
        int[] preMin = new int[nums.length+1];
        preMin[0] = 0;
        for(int i = 0; i < nums.length; i++) {
            s[i+1] = s[i] + nums[i];
        }
        int result = -10000;
        // preMin 是前缀和最小值，那么s[i] - preMin[j]则为最大子数组和。
        for(int i = 1; i < s.length; i ++) {
            preMin[i] = Math.min(preMin[i -1], s[i]);
            // 更新最大和 = s[i] - preMin[i-1] 至少包含第i个元素
            result = Math.max(result, s[i] - preMin[i-1]);
        }

        return result;        
    }
}

解题思路二

通过贪心算法，维护双指针，当子数组和为负数，立即舍弃，慢指针前进，否则快指针已知前进直到数组尾。

二维前缀和

二维数组A (m*n)，其前缀和s[i]s[j]为第i行第j列元素左上角、子矩阵的各个元素之和。

递推关系

s[i][j]= s[i-1][j] +s[i][j-1] - s[i-1]s[j-1] + A[i][j]

子矩阵和

以[p][q]为左上角元素，[i][j]为右下角元素的子矩阵的元素和。

递推关系

sum(p,q,i,j) = s[i][j] +s[i][q-1] - s[p-1]s[j] + s[p-1][q-1]

其中，p，q总是需要减一。

二位区域和检索——矩阵不可变

LC304题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class NumMatrix {

    public NumMatrix(int[][] matrix) {
        n = matrix.length;//row number;
        m = matrix[0].length; // col number;
        sum = new int[n+1][m+1];
        // 二维数组前缀和
        for(int i = 1; i <= n ; i ++){
            for(int j = 1; j <= m; j++) {
                sum[i][j] = sum[i - 1][j] + sum[i][j-1] -sum[i-1][j-1]+ matrix[i-1][j-1];
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        row1++;
        row2++;
        col1++;
        col2++;
        // 索引加一，符合前缀和数组1开头算法。
        return sum[row2][col2] - sum[row1-1][col2] - sum[row2][col1-1] + sum[row1-1][col1-1];
    }

    int sum[][];
    int n, m;
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

差分

差分数组B是由数组的元素差组成的，其中第i元素等于原数组A第i元素与第i-1元素或0的差。

递推关系

B[1] = A[1]

B[i] = A[i -1]

  • 差分数组的前缀和就是原数组
  • 把A数组的第l到第r元素均加d，对应的B变化为B[l]加d，B[r+1]减d。

航班预定统计

LC1109题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int[] corpFlightBookings(int[][] bookings, int n) {
        int[] delta = new int[n+2];
        for(int i = 0; i < n+2; i ++) delta[i] = 0;
        for(int i = 0; i < bookings.length; i++){
            int[] booking = bookings[i];
            int first = booking[0];
            int last = booking[1];
            int seats = booking[2];
            delta[first] += seats; // += 纵向累加delta，seats是diff booking[][first] - booking[first-1]
            delta[last+1] += -seats;  // -seats 是 booking[]last+1] - booking[last] 
        }
        int[] sum = new int[n];
        for(int i = 0;i < n; i++) sum[i] = delta[1];
        for(int i = 1; i < n; i++){
            sum[i] =  sum[i-1] + delta[i+1];
        }
        return sum;
    }
}

/* O(m+n)
1  2  3  4  5
10   -10
   20   -20
   25
10 55 45 25 25
*/

双指针扫描

两数之和II —— 输入有序数组

LC167题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int j = numbers.length -1;
        for(int i = 0; i < numbers.length; i++) {
            while(i < j && numbers[i] + numbers[j] > target) j--;
            if(i < j && numbers[i] + numbers[j] == target) {
                return new int[]{i+1, j+1};
            }
        }
        return new int[]{};
    }
// O(n)
// 2 7 11 15 17 target = 18
// i         j 小于18停止左移动j，检查
//   i j     
//     i  j    小于18停止左移动j，检查
// i 移动时，j单调递减、递增。

}

两数之和

LC1题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
    public int[] twoSum(int[] nums, int target) {
            Pair[] sorted = new Pair[nums.length];
            for(int i = 0; i < nums.length; i ++) sorted[i]= new Pair(i, nums[i]);
            Arrays.sort(sorted);
            int j = nums.length-1;
            for(int i = 0; i < nums.length; i++){
                while(i < j && sorted[i].value + sorted[j].value > target) j--;
                if(i < j && sorted[i].value + sorted[j].value == target) return new int[]{sorted[i].index, sorted[j].index};
            }
            return new int[]{};
        }
        

    static class Pair implements Comparable<Pair> {
        public final int index;
        public final int value;

        public Pair(int index, int value) {
            this.index = index;
            this.value = value;
        }

        @Override
        public int compareTo(Pair other) {
            //multiplied to -1 as the author need descending sort order
            return Integer.valueOf(this.value).compareTo(other.value);
        }
    }
}

三数之和

LC15题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
            Arrays.sort(nums);// 顺序不再重要
            List<List<Integer>> result = new ArrayList<>();
            for(int i = 0; i < nums.length; i++){
                if(i != 0 && nums[i] == nums[i-1]) continue;// 去除第一位重复
                List<List<Integer>> twoSumResults = twoSum(nums, i + 1, -nums[i]);
                for(List<Integer> twoSumResult : twoSumResults){
                    result.add(Arrays.asList(nums[i], twoSumResult.get(0), twoSumResult.get(1)));
                }


            }
            return result;
        }

        List<List<Integer>> twoSum(int[] nums, int start, int target) {
            List<List<Integer>> result = new ArrayList<>();
            int j = nums.length-1;
            for(int i = start; i < nums.length; i++){
                if(i != start && nums[i] == nums[i-1]) continue;// 去除第二位重复
                while(i < j && nums[i] + nums[j] > target) j--;
                if(i < j && nums[i] + nums[j] == target) {
                    List<Integer> finding = new ArrayList<>();
                    finding.add(nums[i]);
                    finding.add(nums[j]);
                    result.add(finding);
                }
            }
            return result;
        }
}

盛最多水的容器

LC11题目链接

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxArea(int[] height) {
        int i = 0, j = height.length-1, ans = 0;
        while( i < j){
            ans = Math.max(ans, Math.min(height[i], height[j])* (j-i));
            // i j 两个指针相遇问题，如果height[i]较矮，则前进i寻找更高的，否则前进j
            if(height[i] < height[j]) i++; else j--;
        }
        return ans;
    }
}

递归

递归的三个关键：

  • 定义需要递归的问题（重叠子问题）—— 数学归纳法思想
  • 确定递归边界
  • 保护与还原现场

递归实现的“暴力搜索”或者叫枚举、回溯方法的基本复杂度为：

递归形式 时间复杂度规模 问题举例
指数型 k^n 子集、大体积背包
排列型 n! 全排列、旅行商、N皇后
组合型 n!/(m!(n-m)!) 组合选数

子集

LC78题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        n = nums.length;
        recur(nums,0);
        return ans;
    }

    void recur(int[] nums, int i){
        // 递归边界
        if(i == n) {
            ans.add(new ArrayList<>(chosen));// 不可加入引用必须复制副本
            return;
        }

        // i 不选
        recur(nums, i+1);

        // i 选中
        chosen.add(nums[i]);
        recur(nums, i+1);
        chosen.remove(chosen.size()-1);
    }


    private int n;
    List<Integer> chosen = new ArrayList<>();
    List<List<Integer>> ans = new ArrayList<>();
}

组合

LC77题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        this.n = n;
        this.k = k;
        recur(1);
        return ans;
    }

    void recur( int i){
        if(chosen.size() > k || chosen.size() + (n -i + 1) <k ) return; // *** 提早退出，剪枝，已经超过k个，或者剩下全选也不够k个
        // 递归边界
        if(i == n+1 ) {
            if(chosen.size() == k) ans.add(new ArrayList<>(chosen));// 不可加入引用必须复制副本
            return;
        }

        // i 不选
        recur(i+1);

        // i 选中
        chosen.add(i);
        recur(i+1);
        chosen.remove(chosen.size()-1);
    }


    private int n, k;
    List<Integer> chosen = new ArrayList<>();
    List<List<Integer>> ans = new ArrayList<>();
}

全排列

LC46题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        this.n = nums.length;
        this.used = new boolean[n];
        recur(nums, 0);
        return ans;
    }
    
    void recur(int[] nums, int pos) {
        // pos 为选中的数字个数
        if(pos == n) {
            ans.add(new ArrayList<>(a));
            return;
        }

        for(int i = 0; i < n; i++) {
            if(!used[i]){
                a.add(nums[i]);
                used[i] = true;
                recur(nums, pos +1 );
                // 还原，从而其他递归分支可以继续计算。
                used[i] = false;
                a.remove(a.size()-1);
            }
        }
    }
    boolean[] used;
    List<Integer> a = new ArrayList<>();
    int n;
    List<List<Integer>> ans = new ArrayList<>();
}

全排列II

LC47题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        this.n = nums.length;
        this.used = new boolean[n];
        Arrays.sort(nums);
        // nums 排序，则在used统计中，要检查所有同样的数字的used情况
        // 拆分成第一个数，和剩下的全排列
        // 如果已经算过该数了，则跳过
        recur(nums, 0);       
        return ans;
    }

    void recur(int[] nums, int pos) {
        // pos 为选中的数字个数
        if(pos == n) {
            ans.add(new ArrayList<>(a));
            return;
        }

        for(int i = 0; i < n; i++) {
            //if(!used[i]){
            if (used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])) {
                continue;
            }
            a.add(nums[i]);
            used[i] = true;
            recur(nums, pos +1 );
            // 还原，从而其他递归分支可以继续计算。
            used[i] = false;
            a.remove(a.size()-1);
            //}
        }
    }
    boolean[] used;
    List<Integer> a = new ArrayList<>();
    int n, first;
    List<List<Integer>> ans = new ArrayList<>();
    Map<Integer, Boolean> record = new HashMap<>();
}

树

反转二叉树

LC226题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;
        TreeNode cache = root.left;
        root.left = root.right;
        root.right = cache;

        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

验证二叉搜索树

LC98题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
     public boolean isValidBST(TreeNode root) {
         // 注意Integer.MIN_VALUE-1 与Integer.MAX_VALUE+1越界问题，用long
            return isValidBST(root, Integer.MIN_VALUE, Integer.MAX_VALUE);
        }

        boolean isValidBST(TreeNode root, long low, long up) {
            if(root == null ) return true;

            if (root.val > up || root.val < low) return false;
            return isValidBST(root.left, low, (long)root.val -1) && isValidBST(root.right, (long)root.val + 1, up);
        }
}

二叉树的最大、最小深度

LC104题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) +1;
    }
}

LC111题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) return 0;
        if (root.left == null) return minDepth(root.right)+1;
        
        if (root.right == null) return minDepth(root.left)+1;
        
        return Math.min(minDepth(root.left), minDepth(root.right)) +1;
    }
}

分治

把原问题划分成若干个同类子问题，分别解决后，再把结果合并起来。

关键点：
原问题和各个子问题都是重复的（同类的）——递归定义
除了向下递归“问题”，还要向上合并“结果”

分治算法一般用递归实现，分为三步骤：

  • 递归边界定义
  • split：分解成多个子问题
  • merge：合并子问题结果

Pow(x,n)

LC50题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public double myPow(double x, int n) {
        // 边界问题
        // 停止
        if(n == 0) return 1;
        // 负数边界，必须再负数之前，否则StackOverflow
        if (n == Integer.MIN_VALUE) return 1.0/ (myPow(x, -(n + 1)) *x);
         // 负数
        if (n < 0) return 1.0/ myPow(x, -n);
        double temp = myPow(x, n/2);
        double ans = temp * temp;
        // 奇数，除以2取整，然后补一个*x
        // 偶数，直接相乘
        if(n%2 == 1) ans *= x;
        return ans;
    }
}

括号生成

LC22题目链接

组合型递归问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ans = new ArrayList<>();
            // boundary
            if(n == 0) return Arrays.asList(new String[]{""});
            if (store.containsKey(n)) return store.get(n);
            // split
            for (int k =1; k <= n; k++ ){ // 加法原理
                List<String> A = generateParenthesis(k-1);
                store.put(k-1, A);
                List<String> B = generateParenthesis(n-k);
                store.put(n-k, B);
                // S=(A)B merge
                // 乘法原理
                for(String a : A ){
                    for(String b: B) {
                        ans.add("(" + a + ")" + b);
                    }
                }
            }
            return ans;
        
    }

    Map<Integer, List<String>> store = new HashMap<>();
}

/*
n = 3

((()))
(()())


(())()
()()()

n = 3

重复问题
--|---- ()(()) ()()()
----|-- (())() ()()()

解决办法：找到第一个不可划分的整体

左侧第一个被一组括号包住，左侧k个括号则为(k-1个括号组合)n-k个括号组合
S (A) B
n k-1 n-k

k=1 (A) A=0对括号       B=n-k=2对括号 ()() (())
()()()  ()(())

k=2 (A) A=1对括号 (())  B=n-k=1对括号 ()
(())()

k=3 (A) A=2对括号 (()())  ((()))  B=n-k=0对括号
(()())   ((()))

总共2+1+2=5种
*/

搜索二维矩阵

LC74题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // 按行搜索直到 target>= matrix[i-1][0] && target <= matrix[i][0]
        // 按列搜索直到 target == matrix[i-1][j]
        int i = 0;
        for( ;i < matrix.length; i++) {
            if(target >= matrix[i][0] && ( i == matrix.length -1 || target < matrix[i+1][0])) break;
        }

        for(int j = 0; j < matrix[0].length; j++) {
            if(i < matrix.length && target == matrix[i][j]) return true;
        }
        return false;
    }
}

合并K个升序链表

LC23题目链接

拆分问题，先合成两个k/2组成的链表,把这两个链表合成k个组成的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        return merge(lists, 0, lists.length -1);
    }

    public ListNode merge(ListNode[] lists, int start, int end) {
        if( start == end) return lists[start];
        if ( start > end ) return null;
        int mid = (start + end) /2;
        return mergeTwoLists(merge(lists, start, mid), merge(lists, mid +1, end));
    }

    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode cur1 = list1, cur2 = list2, nextHead2 = null, protect = new ListNode(0, list1),lastHead1 = protect;
        while(cur1 != null || cur2 != null) {           
            // 更新节点
            if(cur1 == null || (cur2 != null && cur1.val > cur2.val)){ // 取list2节点,cur2 推进
                // 先缓存即将推进的节点
                nextHead2 = cur2.next;
                // cur2 插入在cur1之前,lastHead1之后       
                cur2.next = cur1;               
                lastHead1.next = cur2;
                // 更新lastHead1 和cur2 指针          
                lastHead1 = cur2;
                cur2 = nextHead2;                
            } else { //取list1节点，cur1直接推进
                lastHead1 = cur1;
                cur1 = cur1.next;
            }
        }
        return protect.next;
    }
}

为运算表达式设计优先级

LC241题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
class Solution {

    static final int ADDITION = -1;
        static final int SUBTRACTION = -2;
        static final int MULTIPLICATION = -3;

        public List<Integer> diffWaysToCompute(String expression) {
            ArrayList<Integer> ops = new ArrayList<>();
            // 创建操作数数组 [ 2, -, 1, -, 1]
            for(int i =0; i < expression.length();) {
                if(expression.charAt(i) == '+'){
                    ops.add(ADDITION);
                }else if (expression.charAt(i) == '-'){
                    ops.add(SUBTRACTION);
                }else if (expression.charAt(i) == '*' ){
                    ops.add(MULTIPLICATION);
                }else {
                    int number = 0;
                    while(i < expression.length() && expression.charAt(i) <= '9' && expression.charAt(i) >= '0' ){
                        // 表达式要正确
                        number = 10 * number +  expression.charAt(i) - '0';
                        i++;
                    }
                    ops.add(number);
                    continue;
                }
                i++;
            }

            // 分治法合并表达式
            // split 拆分成两个子数组, [start, mid] [mid + 2, end] 分别得到结果
            // merge 用 mid +1 的符号合并左右子数组的所有可能结果
            // 对于每一层，共有 (start + end )/2 种拆分方式，每次步长为2

            // 缓存结果达到剪枝效果
            // 注意for循环时候不能修改dp本身

            List<Integer>[][] dp = new List[ops.size()][ops.size()];
            for (int i = 0; i < ops.size(); i++) {
                for (int j = 0; j < ops.size(); j++) {
                    dp[i][j] = new ArrayList<Integer>();
                }
            }

            return dfs(dp, 0, ops.size() -1, ops);
        }

        public List<Integer> dfs(List<Integer>[][] dp, int start, int end, List<Integer> ops){
            if( start > end) return new ArrayList<>();
            if(!dp[start][end].isEmpty()) return dp[start][end];
            // boundary
            if( start == end) {
                dp[start][end].add(ops.get(start));
                return Arrays.asList(ops.get(start));
            }
            // split
            for(int mid = start; mid < end; mid+=2){
                List<Integer> leftResults = dfs(dp, start, mid, ops);
                List<Integer> rightResults = dfs(dp, mid+2, end, ops);


                // merge
                for(Integer left : leftResults){
                    for(Integer right : rightResults){
                        if(ops.get(mid+1) == ADDITION) dp[start][end].add(left + right);
                        if(ops.get(mid+1) == SUBTRACTION) dp[start][end].add(left - right);
                        if(ops.get(mid+1) == MULTIPLICATION) dp[start][end].add(left * right);
                    }
                }
            }
            return dp[start][end];
        }

    }

给表达式添加运算符

LC282题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

class Solution {

        List<String> ans = new ArrayList<>();
        int n, target;
        String num;
        public List<String> addOperators(String num, int target) {
            this.n = num.length();
            this.target = target;
            this.num = num;
            long sum = 0, pre = 0;
            dfs(0, 0, "", 0);
            return ans;
        }

        private void dfs(long sum, long pre, String exp, int start){
            //boundary
            if(start == n) {
                if(sum == target)
                    ans.add(exp);
                return;
            }

            // main logic, loop from start to n-1 with sum = xxx
            // 右操作数有四种选择
            // 直接拼接
            // + - *
            // int val 会有越界问题
            long val = 0 ;
            for(int i = start; i < n; i++) {
                // 开头是0 (num.charAt(start) 则不处理拼接的情况。
                if(i != start && num.charAt(start) == '0')
                    break;

                val = val* 10 + num.charAt(i) - '0';

                if(start == 0) {
                    dfs(val, val, exp + val, i+1);
                }else {
                    // sum[i] =  sum[i-1] + val
                    dfs(sum + val, val, exp + "+" + String.valueOf(val), i+1);
                    // sum[i] =  sum[i-1] - val
                    dfs(sum - val, -val, exp + "-" + String.valueOf(val), i+1);
                    // sum[i] =  sum[i-1] - pre + val*pre
                    dfs(sum - pre + pre * val, pre * val, exp + "*" + String.valueOf(val), i+1);
                }
            }
        }
/*

  递归法解决问题：

  num拆分成字符串，长度为n。

  第i-1层到第i层递进递归：

  1. 边界
    如果start == n 及 存入满足target条件的表达式。
  2. split
    需要知道当前层的和，i-1 层的乘积，当前表达式，把运算结果直接当参数传入下层，从而减轻解析计算复杂度。
    dfs(long sum, long pre, String exp, int start)

    123 为例 展开为：

    1 + f(23)
    1 + f(2) + f(3)
    12 + f(3)
// 提示：
具体来说，我们枚举连续数字(即一个数字段)的长度(长度大于111，即中间什么都不插入)，然后考虑和上一段数字之间中间的二元运算符是什么。

假如递归枚举到第iii段数字的时候，考虑二元运算符三种情况。设前i−1i-1i−1段数字的表达式和为sumsumsum。

第一种，中间是+++，则sumsumsum加上第iii段数字。
第二种，中间是−-−，则sumsumsum减去第iii段数字。
第三种，中间是×××，则sumsumsum减去上一段连续乘的值(因此我们需要在递归的时候记录上一段的值，对于第iii段数字，即记录第i−1i-1i−1的数字是多少)，再加上 第i−1i-1i−1段数字×第iii段数字。(例如，1+2×3×41+2×3×41+2×3×4，假设当前枚举3和4之间的运算符，是×运算符，则sumsumsum减去2×3=62×3=62×3=6，然后加上2×3×4=242×3×4=242×3×4=24)。
注意，连续000的情况要特殊处理。
*/

    }

数组中的第K个最大元素

LC215题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int findKthLargest(int[] nums, int k) {
        Pair[] sorted = new Pair[nums.length];
        for(int i = 0; i < nums.length ; i++) sorted[i] =  new Pair(i, nums[i]);
        Arrays.sort(sorted);
        return sorted[k-1].value;
    }

    static class Pair implements Comparable<Pair>{
        int index, value;
        public Pair(int index, int value) {
            this.index = index;
            this.value = value;
        }

        @Override
        public int compareTo(Pair other){
            return other.value - this.value;
        }
    }
}

综合习题

和为 K 的子数组

LC560题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    public int subarraySum(int[] nums, int k) {
        int[] s = new int[nums.length+1];
        s[0] = 0;
        Map<Integer, Integer> count = new HashMap<>();
        count.put(0, 1);
        // 前缀和
        int result = 0;
        for(int i = 1; i <= nums.length; i++) {
            s[i] = s[i-1] + nums[i-1];            
            // !!必须在没有全部s数组前机型计算，避免各种边界，例如i< j, k =0 之类
            result += count.getOrDefault(s[i] - k, 0);
            count.put(s[i], count.getOrDefault(s[i], 0)+1);
        }
        // 存入count[s[i]]的个数
        // s[i] - s[j] == k 等价于
        // count[s[i] - k] 的个数
        // i 必须 >= j
        return result;
    }


}

最接近原点的 K 个点

LC973题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

class Solution {
    public int[][] kClosest(int[][] points, int k) {
        // this.k = k;
        sorted = new Pair[points.length];
        // 存入所有distance，排序后取前k个。
        for(int i = 0; i < points.length; i++) {
            enqueue(points, i);
        }
        Arrays.sort(sorted);
        int[][] result = new int[k][2];
        int current = 0;
        for(int j = 0; j < k;j++){
            result[current][0] = points[sorted[j].index][0];
            result[current][1] = points[sorted[j].index][1];
            current ++;
        }
        return result;
    }

    private void enqueue(int[][] points, int index) {
        int distance = getDistance(points, index);
        sorted[index] = new Pair(index, distance);
        //dMap.put(index, distance);
        // 算法超时： // 找到第一个小于的位置放入，保证队列不找过k个元素。
        // int r;
        // for(r = 0; r < q.size() && !q.isEmpty(); r++) {
        //     if(distance <= dMap.get(q.get(r))) {
        //         q.add(r, index);
        //         if(q.size() > k) q.removeLast();
        //         break;
        //     }
        // }

        // if(q.isEmpty()) q.add(index);
        // if(q.size() < k && r == q.size()) q.addLast(index);
    }

    private int getDistance(int[][] points, int index) {
        return points[index][0]*points[index][0] + points[index][1]*points[index][1];
    }
    // 单调递减队列，只有k个容量
    LinkedList<Integer> q = new LinkedList<>();
    // Map<Integer,Double> dMap = new HashMap<>();
    Pair[] sorted;
    // int k ;

    static class Pair implements Comparable<Pair> {
        public final int index;
        public final int value;

        public Pair(int index, int value) {
            this.index = index;
            this.value = value;
        }

        @Override
        public int compareTo(Pair other) {
            //multiplied to -1 as the author need descending sort order
            return Integer.valueOf(this.value).compareTo(other.value);
        }
    }
}

鸡蛋掉落

LC887题目链接

解题思路：

  1. 回溯：递归展开，dp归纳法得出最优解
  2. 记忆化剪枝优化
  3. 根据其单调性二分查找快速定位最大值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

class Solution {
    public int superEggDrop(int k, int n) {
        return recur(k, n); 
    }
    
    private int recur(int K, int N) {
        // boundary
        // K == 1 needs tranverse every floor with the only egg
        // N == 0 or 1 needs 1 time to do
        if(K == 1 || N == 0 || N == 1) {
            return N;
        }
        
        //Pair key = new Pair(K, N);
        int key = 1000*N +K;
        if(memo2.containsKey(key)) return memo2.get(key);
        // dp
        /* transition function
        searchTime(K, N) = max( searchTime(K-1, X-1), searchTime(K, N-X) )
        min = min(searchTime(K, N), min)
        */
        //int min = N;    // inital max is N
        
        // recur(K -1, X-1) means egg breaks
        // recur(K, N - X) means egg not break
        // sequential search time exceeded!
        // binary search as recur(K-1, X-1) monolithic increasing with X grow
        // max KN should be around middle
        //for(int X = 1; X <= N; X++){
        int low = 1, high = N;
        int X = 0;
        while(low +1 < high){
            X = (low + high)/2;
            int KNlow = recur(K-1, X-1);
            int KNhigh = recur(K, N-X);
            if(KNlow < KNhigh) low = X;
            else if(KNlow > KNhigh) high = X;
            else low = high = X;
            
        }
        
        int KN = Math.max( recur(K-1, low-1), recur(K, N-low) );
        int KN2 = Math.max(recur(K-1, high-1), recur(K, N-high));
        // KN + 1 means executed once;
        int min = Math.min(KN, KN2)+1;
        //}
        
        // K = 2, N = 3
        // X = 1; r(1, 0)=0 r(2, 2)=? 2
        // X = 2; r(1, 1)=1 r(2, 1)=1
        // K = 2, N = 2
        // X = 1; r(1, 0)=1 r(2, 1)=2
        // X = 2; r(1, 1)=2 r(2, 0)=1
        // r(2, 2) = 1
        // cache result 
        memo2.put(key, min);
        return min;
    }
    
    //Map<Pair, Integer> memo = new HashMap<>();
    Map<Integer, Integer> memo2 = new HashMap<>();
    
    // static class Pair{
    //     int K, N;
    //     public Pair(int K, int N){
    //         this.K = K;
    //         this.N = N;
    //     }
        
    //     @Override
    //     public int hashCode(){
    //         return 100 * N + K;
    //     }
    // }
}

发表于 更新于 分类于 ，

Jetty I/O Model

Jetty是一个开源的轻量级webserver框架，实现了大部分javax标准下的接口，并且也提供了很多有用的协议支持，例如http1.1， http2， 和websocket等。Jetty采用了最新的Java Nio接口，从底层解决了阻塞式处理I/O的问题，利用SelectionKey实现了多路复用socketChannel，得到了高效的I/O吞吐性能。本文将着重从源代码层面去讲解Jetty是如何做到。

Jetty Server

Jetty Server实例是整个服务的容器，包含了connectors负责管理客户端连接。

Jetty ServerConnector

ServerConnector扩展了既有的AbstractConnector，实现了异步处理ServerSocketChannel的selectedKeys事件回调。主要是通过SelectorManager管理一系列ManagedSelector，根据不同的协议生成不同的连接实例。

Jetty AbstractConnector

AbstractConnector是Connector的基本实现，主要包含了一组ConnectionFactory负责构造不同类型的connection，也包含了一组AbstractCoonector.Acceptor实例,负责监听所有的accept事件，accept事件是客户端连接的第一个事件。

Jetty SelectorManager与ManagedSelector

SelectorManager是所有ManagedSelector的管理员，负责异步执行所有ManagedSelector提交的Task，是多路复用一个ServerSocketChannel的核心。底层是依赖Java Nio的ServerSocketChannel多路复用技术实现。

Java Nio的多路复用技术

Reference

  • ServerSocketChannel

    • 创建：通过ServerSocketChannel类的静态方法open()获得。
    • 绑定端口：每个ServerSocketChannel都有一个对应的ServerSocket,通过其socket()方法获得。获得ServerSocket是为了使用其bind()方法绑定监听端口号。若是使用其accept()方法监听请求就和普通Socket的处理模式无异。
    • 设置是否使用阻塞模式：true/false。configureBlocking(false)——不适用阻塞模式。阻塞模式不能使用Selector！
    • 注册选择器以及选择器关心的操作类型：register(Selector,int) 第一个参数可以传入一个选择器对象，第二个可传入SelectionKey代表操作类型的四个静态整型常量中的一个，表示该选择器关心的操作类型。

  • Selector

    • 创建：通过Selector的静态方法open()获得。

    • 等待请求：select(long)——long代表最长等待时间，超过该时间程序继续向下执行。若设为0或者不传参数，表示一直阻塞，直到有请求。

    • 获得选择结果集合：selectedKeys()，返回一个SelectionKey集合。SelectionKey对象保存处理当前请求的Channel、Selector、操作类型以及附加对象等等。
      SelectionKey对象有四个静态常量代表四种操作类型以及对应的判断是否是该种操作的方法：

      • SelectionKey.OP_ACCEPT——代表接收请求操作 isAcceptable()

      • SelectionKey.OP_CONNECT——代表连接操作 isConnectable()

      • SelectionKey.OP_READ——代表读操作 isReadable()

      • SelectionKey.OP_WRITE——代表写操作 isWritable()

  • NioSocket中服务端的处理过程分为5步：

    1. 创建ServerScoketChannel对象并设置相关参数（绑定监听端口号，是否使用阻塞模式）
    2. 创建Selector并注册到服务端套接字信道（ServerScoketChannel）上
    3. 使用Selector的select方法等待请求
    4. 接收到请求后使用selectedKeys方法获得selectionKey集合
    5. 根据选择键获得Channel、Selector和操作类型进行具体处理。

  • Code Sample

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
/*
模拟服务端 -nio-Socket 实现
*/
public class  NIOServer  {
    public static void  main ( String []  args ) {
        try  {
            // 创建 ServerSocketChannel 通道，绑定监听端口为 8080
            ServerSocketChannel  serverSocketChannel =  ServerSocketChannel . open () ;
            serverSocketChannel. socket ().bind( new  InetSocketAddress( 8080 )) ;
            // 设置为非阻塞模式
            serverSocketChannel.configureBlocking( false ) ;
            // 注册选择器 , 设置选择器选择的操作类型
            Selector  selector =  Selector . open () ;
            serverSocketChannel.register(selector ,  SelectionKey . OP_ACCEPT ) ;
            // 创建处理器
            Handler  handler =  new  Handler( 1204 ) ;
            while  ( true ) {
                // 等待请求，每次等待阻塞 3s ，超过时间则向下执行，若传入 0 或不传值，则在接收到请求前一直阻塞
                if  (selector. select ( 3000 ) ==  0 ) {
                    System . out .println( " 等待请求超时 ......" ) ;
                    continue ;
                }
                System . out .println( "----- 处理请求 -----" ) ;
                // 获取待处理的选择键集合
                Iterator< SelectionKey > keyIterator = selector. selectedKeys (). iterator () ;
                while  (keyIterator. hasNext ()) {
                    SelectionKey  selectionKey = keyIterator. next () ;
                    try  {
                        // 如果是连接请求，调用处理器的连接处理方法
                        if (selectionKey.isAcceptable()){
                            handler.handleAccept(selectionKey) ;
                        }
                        // 如果是读请求，调用对应的读方法
                        if  (selectionKey.isReadable()) {
                            handler.handleRead(selectionKey) ;
                        }
                    }  catch  ( IOException  e ) {
                        keyIterator. remove () ;
                        continue ;
                    }
                }
                // 处理完毕从待处理集合移除该选择键
                keyIterator. remove () ;
            }
        }  catch  ( IOException  e ) {
            e .printStackTrace() ;
        }
}

    /*
        处理器类
    */
    private static class  Handler {
        private int  bufferSize  =  1024 ;  // 缓冲器容量
        private  String  localCharset  =  "UTF-8" ;  // 编码格式

        public  Handler (){}
        public  Handler ( int  bufferSize ){
            this ( bufferSize , null ) ;
        }
        public  Handler ( String  localCharset ){
            this (- 1 , localCharset ) ;
        }
        public  Handler ( int  bufferSize , String  localCharset ){
            if ( bufferSize  >  0 ){
                this . bufferSize  =  bufferSize ;
            }
            if ( localCharset  !=  null ){
                this . localCharset  =  localCharset ;
            }
        }
        /*
        连接请求处理方法
        */
        public void  handleAccept ( SelectionKey  selectionKey )  throws  IOException  {
            // 通过选择器键获取服务器套接字通道，通过 accept() 方法获取套接字通道连接
            SocketChannel  socketChannel = (( ServerSocketChannel ) selectionKey . channel ()). accept () ;
            // 设置套接字通道为非阻塞模式
            socketChannel.configureBlocking( false ) ;
            // 为套接字通道注册选择器，该选择器为服务器套接字通道的选择器，即选择到该 SocketChannel 的选择器
            // 设置选择器关心请求为读操作，设置数据读取的缓冲器容量为处理器初始化时候的缓冲器容量
            socketChannel.register( selectionKey . selector () , SelectionKey . OP_READ ,  ByteBuffer . allocate ( bufferSize )) ;
        }

        public void  handleRead ( SelectionKey  selectionKey )  throws  IOException  {
            // 获取套接字通道
            SocketChannel  socketChannel = ( SocketChannel )  selectionKey . channel () ;
            // 获取缓冲器并进行重置 ,selectionKey.attachment() 为获取选择器键的附加对象
            ByteBuffer  byteBuffer = ( ByteBuffer ) selectionKey .attachment() ;
            byteBuffer.clear() ;
            // 没有内容则关闭通道
            if  (socketChannel. read (byteBuffer) == - 1 ) {
                socketChannel.close() ;
            }  else  {
                // 将缓冲器转换为读状态
                byteBuffer.flip() ;
                // 将缓冲器中接收到的值按 localCharset 格式编码保存
                String  receivedRequestData =  Charset . forName ( localCharset ). newDecoder ().decode(byteBuffer).toString() ;
                System . out .println( " 接收到客户端的请求数据： " +receivedRequestData) ;
                // 返回响应数据给客户端
                String  responseData =  " 已接收到你的请求数据，响应数据为： ( 响应数据 )" ;
                byteBuffer =  ByteBuffer . wrap (responseData.getBytes( localCharset )) ;
                socketChannel. write (byteBuffer) ;
                // 关闭通道
                socketChannel.close() ;
            }
        }
    }
}

Jetty对socket的多路复用技术实现

Jetty主要是依赖底层Java Nio的多路复用技术，并且封装成为高吞吐量的服务器。封装主要分成两部分：

  • Connector -> Acceptor: 当新的请求到达Jetty时，Jetty ServerConnector会拿到一个非阻塞、新的_acceptChannel：ServerSocketChannel，其关联的selector用于接收所有后续Accept/Update/onSelected/close/ReplaceKey事件。Acceptor作为Selector的回调类，提供了所有socketchannel事件的回调方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
  * Called by {@link #open()} to obtain the accepting channel.
  *
  * @return ServerSocketChannel used to accept connections.
  * @throws IOException if unable to obtain or configure the server channel
  */
 protected ServerSocketChannel openAcceptChannel() throws IOException
 {
     ServerSocketChannel serverChannel = null;
     if (isInheritChannel())
     {
         Channel channel = System.inheritedChannel();
         if (channel instanceof ServerSocketChannel)
             serverChannel = (ServerSocketChannel)channel;
         else
             LOG.warn("Unable to use System.inheritedChannel() [{}]. Trying a new ServerSocketChannel at {}:{}", channel, getHost(), getPort());
     }

     if (serverChannel == null)
     {
         InetSocketAddress bindAddress = getHost() == null ? new InetSocketAddress(getPort()) : new InetSocketAddress(getHost(), getPort());
         serverChannel = ServerSocketChannel.open();
         setSocketOption(serverChannel, StandardSocketOptions.SO_REUSEADDR, getReuseAddress());
         setSocketOption(serverChannel, StandardSocketOptions.SO_REUSEPORT, isReusePort());
         try
         {
             serverChannel.bind(bindAddress, getAcceptQueueSize());
         }
         catch (Throwable e)
         {
             IO.close(serverChannel);
             throw new IOException("Failed to bind to " + bindAddress, e);
         }
     }

     return serverChannel;
 }

  • SelectorManager -> ManagedSelector -> Selector: SelectorManager负责维护一组可以复用的Selector实例，对于每个_acceptChannel：ServerSocketChannel非阻塞实例，可以注册一个Selector实例用于监听相应的SelectionKey事件。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

// 创建一个selector实例,并且用一个新的生产者线程不断监听channel中的事件。
@Override
    protected void doStart() throws Exception
    {
        super.doStart();

        _selector = _selectorManager.newSelector();

        // The producer used by the strategies will never
        // be idle (either produces a task or blocks).

        // The normal strategy obtains the produced task, schedules
        // a new thread to produce more, runs the task and then exits.
        _selectorManager.execute(_strategy::produce);

        // Set started only if we really are started
        Start start = new Start();
        submit(start);
        start._started.await();
    }

  • Selector事件的生产者/消费者模式：选择器本身是可以复用的，也就是大量请求创建的大量socketchannel是可以共享一个选择器实例，并且通过selectedKey.channel()获得相应的channel实例。这相较于传统的一个请求一个线程模式提高了线程利用率，避免了大量请求带来的线程池饥饿问题。同时，selector本身的事件也需要有很好的资源复用，否则，生产者产生的大量任务同时也会让消费者线程饥饿造成阻塞。Jetty为了解决这个问题采用了一种新的消费模式: EPC,即 eat what you kill消费者和生产者同线程优先处理模式。

    ExectuteProduceConsume

    1. SelectorProducer类提供了一个循环loop负责阻塞查询select()并且将查询到的事件/任务提交到_updates队列中。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    @Override
        public Runnable produce()
        {
            while (true)
            {
                Runnable task = processSelected();
                if (task != null)
                    return task;

                processUpdates();

                updateKeys();

                if (!select())
                    return null;
            }
        }
    1. 产生的任务主要分四种:
    • processSelected(): 处理selected事件产生真正的task,或者处理connect事件。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    private Runnable processSelected()
    {
        while (_cursor.hasNext())
        {
            SelectionKey key = _cursor.next();
            Object attachment = key.attachment();
            SelectableChannel channel = key.channel();
            if (key.isValid())
            {
                if (LOG.isDebugEnabled())
                    LOG.debug("selected {} {} {} ", safeReadyOps(key), key, attachment);
                try
                {
                    if (attachment instanceof Selectable)
                    {
                        // Try to produce a task
                        Runnable task = ((Selectable)attachment).onSelected();
                        if (task != null)
                            return task;
                    }
                    else if (key.isConnectable())
                    {
                        processConnect(key, (Connect)attachment);
                    }
                    else
                    {
                        throw new IllegalStateException("key=" + key + ", att=" + attachment + ", iOps=" + safeInterestOps(key) + ", rOps=" + safeReadyOps(key));
                    }
                }
                catch (CancelledKeyException x)
                {
                    if (LOG.isDebugEnabled())
                        LOG.debug("Ignoring cancelled key for channel {}", channel);
                    IO.close(attachment instanceof EndPoint ? (EndPoint)attachment : channel);
                }
                catch (Throwable x)
                {
                    LOG.warn("Could not process key for channel {}", channel, x);
                    IO.close(attachment instanceof EndPoint ? (EndPoint)attachment : channel);
                }
            }
            else
            {
                if (LOG.isDebugEnabled())
                    LOG.debug("Selector loop ignoring invalid key for channel {}", channel);
                IO.close(attachment instanceof EndPoint ? (EndPoint)attachment : channel);
            }
        }
        return null;
    }

    • processUpdates(): 将updates中的所有SelectorUpdate实例处理完，应该是Selector内部的事件，例如Start，DumpKeys，Acceptor，Accept，Connect，CloseConnection，StopSelector等，有update方法实现具体update内容。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
     private void processUpdates()
    {
        try (AutoLock l = _lock.lock())
        {
            Deque<SelectorUpdate> updates = _updates;
            _updates = _updateable;
            _updateable = updates;
        }

        if (LOG.isDebugEnabled())
            LOG.debug("updateable {}", _updateable.size());

        for (SelectorUpdate update : _updateable)
        {
            if (_selector == null)
                break;
            try
            {
                if (LOG.isDebugEnabled())
                    LOG.debug("update {}", update);
                update.update(_selector);
            }
            catch (Throwable x)
            {
                LOG.warn("Cannot update selector {}", ManagedSelector.this, x);
            }
        }
        _updateable.clear();

        Selector selector;
        int updates;
        try (AutoLock l = _lock.lock())
        {
            updates = _updates.size();
            _selecting = updates == 0;
            selector = _selecting ? null : _selector;
        }

        if (LOG.isDebugEnabled())
            LOG.debug("updates {}", updates);

        if (selector != null)
        {
            if (LOG.isDebugEnabled())
                LOG.debug("wakeup on updates {}", this);
            selector.wakeup();
        }
    }
    • updateKeys(): 处理Selectable实例的updateKey和_keys清理
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
     private void updateKeys()
    {
        // Do update keys for only previously selected keys.
        // This will update only those keys whose selection did not cause an
        // updateKeys update to be submitted.
        for (SelectionKey key : _keys)
        {
            Object attachment = key.attachment();
            if (attachment instanceof Selectable)
                ((Selectable)attachment).updateKey();
        }
        _keys.clear();
    }

    • processConnect(key, attachment): 处理connect请求
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
            private void processConnect(SelectionKey key, Connect connect)
    {
        SelectableChannel channel = key.channel();
        try
        {
            key.attach(connect.attachment);
            boolean connected = _selectorManager.doFinishConnect(channel);
            if (LOG.isDebugEnabled())
                LOG.debug("Connected {} {}", connected, channel);
            if (connected)
            {
                if (connect.timeout.cancel())
                {
                    key.interestOps(0);
                    execute(new CreateEndPoint(connect, key));
                }
                else
                {
                    throw new SocketTimeoutException("Concurrent Connect Timeout");
                }
            }
            else
            {
                throw new ConnectException();
            }
        }
        catch (Throwable x)
        {
            connect.failed(x);
        }
    }
    • select(): 阻塞调用Selector.select()方法获取selectionKeys事件。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59

    private boolean select()
       {
           try
           {
               Selector selector = _selector;
               if (selector != null)
               {
                   if (LOG.isDebugEnabled())
                       LOG.debug("Selector {} waiting with {} keys", selector, selector.keys().size());
                       //阻塞等待select()返回
                   int selected = ManagedSelector.this.select(selector);
                   // The selector may have been recreated.
                   selector = _selector;
                   if (selector != null)
                   {
                       if (LOG.isDebugEnabled())
                           LOG.debug("Selector {} woken up from select, {}/{}/{} selected", selector, selected, selector.selectedKeys().size(), selector.keys().size());

                       int updates;
                       try (AutoLock l = _lock.lock())
                       {
                           // finished selecting
                           _selecting = false;
                           updates = _updates.size();
                       }

                       _keys = selector.selectedKeys();
                       int selectedKeys = _keys.size();
                       if (selectedKeys > 0)
                           _keyStats.record(selectedKeys);
                       _cursor = selectedKeys > 0 ? _keys.iterator() : Collections.emptyIterator();
                       if (LOG.isDebugEnabled())
                           LOG.debug("Selector {} processing {} keys, {} updates", selector, selectedKeys, updates);

                       return true;
                   }
               }
           }
           catch (Throwable x)
           {
               IO.close(_selector);
               _selector = null;

               if (isRunning())
               {
                   LOG.warn("Fatal select() failure", x);
                   onSelectFailed(x);
               }
               else
               {
                   if (LOG.isDebugEnabled())
                       LOG.warn("select() failure", x);
                   else
                       LOG.warn("select() failure {}", x.toString());
               }
           }
           return false;
       }

Jetty多协议支持

Jetty的多协议支持包括HTTP0.9 1.1 2.0和ws等等，其实这些协议本质上都是基于TCP/IP层socket协议上的应用层协议，也就是说，在I/O层面都是通过socket协议的握手和通信规则，只是在内容传输上会有不同。例如早期的http协议是不面向连接的，也就是说即使建立了socket连接，也会在http回应发出后被断开，从而在每次http请求产生更多的IO开销。http也可以复用socket连接，只需要池化管理socket连接即可。而websocket协议则是通过http请求后的upgrade请求建立长连接，从而达到双向全双工通信的效果，所以能够高效的利用socket连接。

JettyWebsocketServlet

在socket连接建立后，Jetty会将request真正的进行处理，主要是通过servlet和filter中的逻辑进行内容处理。主要是通过service方法为入口。当Jetty处理完socket连接IO事件processConnect后，会创建CreateEndPoint任务让selectormanager创建客户端点,并且调用newConnection方法->getDefaultConnectionFactory().newConnection方法创建Connection实例，最终调用connectionOpened -> connection.onOpen方法处理不同协议Connection onOpen后续逻辑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

void createEndPoint(SelectableChannel channel, SelectionKey selectionKey) throws IOException
   {
       EndPoint endPoint = _selectorManager.newEndPoint(channel, this, selectionKey);
       Object context = selectionKey.attachment();
       Connection connection = _selectorManager.newConnection(channel, endPoint, context);
       endPoint.setConnection(connection);
       submit(selector ->
       {
           SelectionKey key = selectionKey;
           if (key.selector() != selector)
           {
               key = channel.keyFor(selector);
               if (key != null && endPoint instanceof Selectable)
                   ((Selectable)endPoint).replaceKey(key);
           }
           if (key != null)
               key.attach(endPoint);
       }, true);
       endPoint.onOpen();
       endPointOpened(endPoint);
       _selectorManager.connectionOpened(connection, context);
       if (LOG.isDebugEnabled())
           LOG.debug("Created {}", endPoint);
   }

http请求会采用HttpConnection实例，而websocket会采用NegotiatingClientConnection实例。HTTP协议的handle是基于状态机HttpHandleState实现，根据不同状态生成不同的action，如dispatch/handling/async_error/blocking等。最终request应该会dispatch用到不同servlet的service方法，进行websocket升级处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

public Action handling()
   {
       try (AutoLock l = lock())
       {
           if (LOG.isDebugEnabled())
               LOG.debug("handling {}", toStringLocked());

           switch (_state)
           {
               case IDLE:
                   if (_requestState != RequestState.BLOCKING)
                       throw new IllegalStateException(getStatusStringLocked());
                   _initial = true;
                   _state = State.HANDLING;
                   return Action.DISPATCH;

               case WOKEN:
                   if (_event != null && _event.getThrowable() != null && !_sendError)
                   {
                       _state = State.HANDLING;
                       return Action.ASYNC_ERROR;
                   }

                   Action action = nextAction(true);
                   if (LOG.isDebugEnabled())
                       LOG.debug("nextAction(true) {} {}", action, toStringLocked());
                   return action;

               default:
                   throw new IllegalStateException(getStatusStringLocked());
           }
       }
   }

这是HttpChannel实例中具体的handle方法,负责执行不同的action，其中最主要的就是dispatch方法，负责分发request到不同的servelet进行服务器用户逻辑处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208

public boolean handle()
  {
      if (LOG.isDebugEnabled())
          LOG.debug("handle {} {} ", _request.getHttpURI(), this);

      HttpChannelState.Action action = _state.handling();

      // Loop here to handle async request redispatches.
      // The loop is controlled by the call to async.unhandle in the
      // finally block below.  Unhandle will return false only if an async dispatch has
      // already happened when unhandle is called.
      loop:
      while (!getServer().isStopped())
      {
          try
          {
              if (LOG.isDebugEnabled())
                  LOG.debug("action {} {}", action, this);

              switch (action)
              {
                  case TERMINATED:
                      onCompleted();
                      break loop;

                  case WAIT:
                      // break loop without calling unhandle
                      break loop;

                  case DISPATCH:
                  {
                      if (!_request.hasMetaData())
                          throw new IllegalStateException("state=" + _state);

                      dispatch(DispatcherType.REQUEST, () ->
                      {
                          for (HttpConfiguration.Customizer customizer : _configuration.getCustomizers())
                          {
                              customizer.customize(getConnector(), _configuration, _request);
                              if (_request.isHandled())
                                  return;
                          }
                          getServer().handle(HttpChannel.this);
                      });

                      break;
                  }

                  case ASYNC_DISPATCH:
                  {
                      dispatch(DispatcherType.ASYNC, () -> getServer().handleAsync(this));
                      break;
                  }

                  case ASYNC_TIMEOUT:
                      _state.onTimeout();
                      break;

                  case SEND_ERROR:
                  {
                      try
                      {
                          // Get ready to send an error response
                          _response.resetContent();

                          // the following is needed as you cannot trust the response code and reason
                          // as those could have been modified after calling sendError
                          Integer code = (Integer)_request.getAttribute(RequestDispatcher.ERROR_STATUS_CODE);
                          if (code == null)
                              code = HttpStatus.INTERNAL_SERVER_ERROR_500;
                          _response.setStatus(code);

                          // The handling of the original dispatch failed and we are now going to either generate
                          // and error response ourselves or dispatch for an error page.  If there is content left over
                          // from the failed dispatch, then we try to consume it here and if we fail we add a
                          // Connection:close.  This can't be deferred to COMPLETE as the response will be committed
                          // by then.
                          ensureConsumeAllOrNotPersistent();

                          ContextHandler.Context context = (ContextHandler.Context)_request.getAttribute(ErrorHandler.ERROR_CONTEXT);
                          ErrorHandler errorHandler = ErrorHandler.getErrorHandler(getServer(), context == null ? null : context.getContextHandler());

                          // If we can't have a body, then create a minimal error response.
                          if (HttpStatus.hasNoBody(_response.getStatus()) || errorHandler == null || !errorHandler.errorPageForMethod(_request.getMethod()))
                          {
                              sendResponseAndComplete();
                              break;
                          }

                          dispatch(DispatcherType.ERROR, () ->
                          {
                              errorHandler.handle(null, _request, _request, _response);
                              _request.setHandled(true);
                          });
                      }
                      catch (Throwable x)
                      {
                          if (LOG.isDebugEnabled())
                              LOG.debug("Could not perform ERROR dispatch, aborting", x);
                          if (_state.isResponseCommitted())
                              abort(x);
                          else
                          {
                              try
                              {
                                  _response.resetContent();
                                  sendResponseAndComplete();
                              }
                              catch (Throwable t)
                              {
                                  if (x != t)
                                      x.addSuppressed(t);
                                  abort(x);
                              }
                          }
                      }
                      finally
                      {
                          // clean up the context that was set in Response.sendError
                          _request.removeAttribute(ErrorHandler.ERROR_CONTEXT);
                      }
                      break;
                  }

                  case ASYNC_ERROR:
                  {
                      throw _state.getAsyncContextEvent().getThrowable();
                  }

                  case READ_CALLBACK:
                  {
                      ContextHandler handler = _state.getContextHandler();
                      if (handler != null)
                          handler.handle(_request, _request.getHttpInput());
                      else
                          _request.getHttpInput().run();
                      break;
                  }

                  case WRITE_CALLBACK:
                  {
                      ContextHandler handler = _state.getContextHandler();
                      if (handler != null)
                          handler.handle(_request, _response.getHttpOutput());
                      else
                          _response.getHttpOutput().run();
                      break;
                  }

                  case COMPLETE:
                  {
                      if (!_response.isCommitted())
                      {
                          if (!_request.isHandled() && !_response.getHttpOutput().isClosed())
                          {
                              // The request was not actually handled
                              _response.sendError(HttpStatus.NOT_FOUND_404);
                              break;
                          }

                          // Indicate Connection:close if we can't consume all.
                          if (_response.getStatus() >= 200)
                              ensureConsumeAllOrNotPersistent();
                      }

                      // RFC 7230, section 3.3.
                      if (!_request.isHead() &&
                          _response.getStatus() != HttpStatus.NOT_MODIFIED_304 &&
                          !_response.isContentComplete(_response.getHttpOutput().getWritten()))
                      {
                          if (sendErrorOrAbort("Insufficient content written"))
                              break;
                      }

                      // If send error is called we need to break.
                      if (checkAndPrepareUpgrade())
                          break;
                      
                      // Set a close callback on the HttpOutput to make it an async callback
                      _response.completeOutput(Callback.from(NON_BLOCKING, () -> _state.completed(null), _state::completed));

                      break;
                  }

                  default:
                      throw new IllegalStateException(this.toString());
              }
          }
          catch (Throwable failure)
          {
              if ("org.eclipse.jetty.continuation.ContinuationThrowable".equals(failure.getClass().getName()))
                  LOG.trace("IGNORED", failure);
              else
                  handleException(failure);
          }

          action = _state.unhandle();
      }

      if (LOG.isDebugEnabled())
          LOG.debug("!handle {} {}", action, this);

      boolean suspended = action == Action.WAIT;
      return !suspended;
  }


0%